Claude Shannon Théorie mathématique de la communication
Avant Shannon, on pressentait qu’un message, télégraphique par exemple, pouvait être codifié, transporté, et « redéballé » pour le restituer à l’humain. Les laboratoires Bell travaillaient déjà sur le sujet. Robert Wiener, maître de Shannon, par ses réflexions sur la probabilité des états de transmission d’un signal a influencé cette théorie.
L’apport de Shannon a été de cristalliser des courants de pensée, et les formaliser dans ce texte essentiel.
On n’abordera pas ici les théorèmes relatifs à la capacité d’un canal de communication à transmettre la quantité d’information.
Système de communication.
Claude Shannon définit le système de communication [ schéma de Shannon ] :
Modèle de communication de Shannon
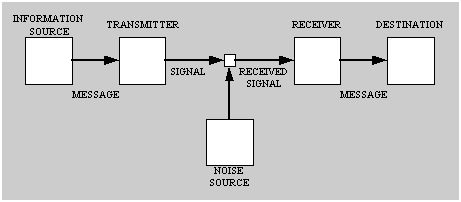
source → encodeur → signal → décodeur → destinataire, dans un contexte de brouillage
L’information.
Shannon définit la notion d’information, d’un point de vue scientifique.
L’information est une mesure scientifique. Elle n’a pas de lien avec la signification en tant que telle d’un message. Il s’agit bien d’une théorie des signaux. On ne s’intéresse pas au sens des messages. C’est ce qui fait la force de cette abstraction. « il n’y a de science que le général ». Shannon refuse la spécificité du message ( sa signification par exemple ) au profit de ses caractéristiques physiquement observables. C’est en cela que « par une série d’élargissements successifs, un modèle de communication partant de l’échange de signes parfaitement définis depuis un point jusqu’à un autre », Claude Shannon a pu intégrer plus globalement ensuite la musique, la parole, l’image.
L’information est une mesure de la liberté de choix, dont on dispose lorsqu’on sélectionne un message. Une mesure mathématique de l’originalité de la situation, créée au récepteur par l’avènement d’un message.
Lorsque j’ai le choix entre 2 messages (« noir » ou « blanc »), j’ai deux possibilités que je représente par 0 ou 1. Plus généralement, la quantité de l’information est définie par le logarithme du nombre des choix possibles. 2 puissance n, lorsqu’il y a n choix possibles. Pour le choix le plus simple, l’unité d’information est 2 (2 puissance 1 ). Cette unité d’information est appelée bit ( mot proposé par John W. Tukey pour « binary digit » ).
De sorte que le « digit binaire » ou « bit » est naturellement associé à une situation de double choix constituant une unité d’information. Dans un système à 3 choix possibles, j’ai 2 puisse 3 soit 8 possibilités, formalisée par 000, 001, 010, 011, 100, 101, 110, 111.
Entropie et probabilités d’information.
Plus on a le choix dans l’élaboration des messages, plus la probabilité de choisir un des messages est forte, et plus grande est l’information. ( entropie forte ).
Plus une situation est hautement organisée et prédictive ( « le soleil se couche en fin de journée »), le hasard ou le choix sont limités, plus l’information ( ou entropie ) est faible.
« La quantité précisément nécessaire à l’établissement de l’information correspond exactement à la notion thermodynamique d’entropie. Elle s’exprime en termes de probabilités. Celles nécessaires pour l’accession à certains stades de processus de formation des messages, et celles une fois ces stades atteints, prévoyant le choix suivant de certains symboles. »
Soit le mot « joie » ; le « e » est déterminé, ne laisse pas le choix à celui qui écrit le mot. Il s’agit de la fraction de structure de message qui est déterminé non par le libre choix de l’émetteur mais plutôt par des règles statistiques admises gouvernant l’emploi des symboles en question ( ici la langue française ). On l’appelle « redondance », car cette fraction du message n’est pas nécessaire, et redondante.
Le bruit.
Le bruit modifie le message, lorsqu’il y a parasite sur une ligne téléphonique par exemple. Une erreur dans la transmission du message. Ces éléments « perturbateurs » de la transmission sont appelés « bruit ». Naturellement on peut penser que le bruit abime le message transmis ( on n’a pas tout entendu ),et donc que l’information transmise diminue . Paradoxalement, l’incertitude du message augmente, et donc l’information.
L’impact de ce texte est fondamental. Sa synthèse d’une dimension communicationnelle de son modèle a inspiré les linguistiques.
Jakobson, par exemple, s’est inspiré du modèle de Shannon , pour structurer les 6 fonctions du langage. Ses études ont elles même marqué les sciences linguistiques.
Au code, émetteur, destinataire, canal, message et bruit, Jakobson en a déduit les fonctions du langage ordinaire : les 6 fonctions du langage de Jakobson
Ce texte reste moderne : aujourd’hui avec les nouveaux réseaux sociaux, ces concepts demeurent.
On lira ainsi : les 6 fonctions de Twitter, selon Jakobson : un exemple appliqué à ce réseau social
Le modèle de Shannon a structuré toute une école de la pensée autour de la communication. On lira cette évolution : l’évolution du concept de la communication.
Claude Shannon : en savoir plus !
Claude Shannon a laissé son nom à un prix décerné chaque année par l’association de la théorie de l’information (IEEE), pour récompenser les avancées sur la théorie de l’information. Site officiel : IEEE Information Theory Society.
Claude Shannon a vraiment bousculé notre monde.
Aujourd’hui, le bit, l’octet ont permis de révolutionner le monde. Notamment le monde numérique : les photos, les textes, les vidéos, et bientôt le monde des objets connectés du monde réel suivent ce même trajet, tracé par Claude Shannon.
D’un point de vue humain, l’être humain est ainsi devenu numérique, extension d’un monde improbable : le bit ou la sueur de la vie numérique